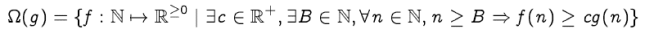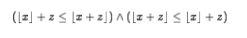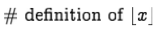csc165 – week 12

Finally, the fall section in U of T ended. CSC165 is one of the courses that I had to challenge. I found myself struggling with some basic mathematical techniques that were used in proof.

Topics in CSC165 were very new concept to me and they were broken down to:
1. Reading and writing with symbols
2. Logic
3. Proof techniques
4. Growth rate questions such as Big O, Big Omega
5. Counting steps of codes

There are some slogs which I often read and have elements that I wish I had included in my slog. For example, Yi’s blog (http://165choi.blogspot.ca) extensively covered the details in solving problems and I admire how Alexandru kept his SLOG updated every single week (http://alexbalutaslog.blogspot.ca).

Overall I really enjoyed learning new concepts in CSC165. It is really well designed course with topics broken down which teaches you mathematical reasoning and expressions step by step. Each topics, I had to fully understand previous materials very well in order to understand the next topic.

csc165 – week 11

This week is fall break and we learnt about halting problem. It is believed to be the most difficult topic in csc165. I can’t think of any details to write about as I am still confused, but here’s one question from assignment 3.

Problem solving episode:
Step 1: Claim : the function meaning_of_life is non-computable.
Proof by reduction:

For a contradiction, assume that meaning_of_life is computable,i.e. It can be implemented as a python function. So, implement halt(f, n) using meaning_of_life(f, I),

def halt(g, i):

     def meaning_of_life(f, I):

         …code for meaning_of_life goes here…

     def g_prime(x):

         g(i)

         return 42

return meaning_of_life(g_prime, i)

If g(i) halts, then g_prime(i) will execute the statement return 42, so meaning_of_life(g_prime, i) returns True, so halt(g, i) returns True.

If g(i) does not halt, then g_prime(i) will not execute the statement return 42(no matter what value x has), then meaning_of_life(g_prime, i) returns False, then halt(g, i) returns False.

But there is no python implementation of function halt.

Hence, there is no python implementation of function meaning_of_life.

csc165 – week 10

This week, we moved on to proving statements with Big-Omega, which are pretty similar to Big-Oh statements. In fact, they’re the same, but in opposites “direction”, i.e f ∈O(g) can also be written g ∈Ω( f ), meaning that a function g that is in Big-Omega of another function f implies that g is an upper bound of f.  The Big-Omega in “statement form” is almost the same as Big-Oh, except the last inequality: Also, to prove this statement, we have to underestimate g(n) and come up with a c to introduce an overestimated version of f(n) to move on with the proof (the opposite way of proving Big-Oh). We also learned about proving general statements with Big-Oh, Big-Omega and Big-Theta together. I found those general proofs to be as interesting as the specific proofs, and the general concept is the same.

Problem solving episode:
Step 1: write a detailed structured proof of: 
Step 2: The statement means that if there is a function f that is upper bounded by function g and if that function g is upper bounded by function h, it implies that function f is also upper bounded by function h. The statement intuitively looks true, because this is a basic rule of transitivity.
Step 3:

Step 4: The proof looks good as f2 and g2 are defined in the way: all n in N, f2(n)=f(n), and similarly for g(n)

We learned more of bounding of functions this week. Since, there exist of an upper bound(big O) there should be lower bound for function. This lower bound is called big omega(Ω). This definition is saying g grows at least as fast as f thus it is lower bound. Also, there is average of growth rate which called big theta(Θ).  In this case, growth rate f is bounded below and above by g. In another words, g grows as same rate as f.

csc165 – week 9

This week, we learnt about disproving statements about Big-Oh. It turned out to be similar, and in order to do that we have to negate the statement linked with f∈O(g) so that it becomes f∉O(g):

Now so far, we had only seen Big-Ohs of polynomials, and it is pretty easy to figure out whether a function is in Big-Oh of another function simply by looking at the highest degrees of the two functions. But for non-polynomials, we have to use limits. The below diagram is taken from one of Larry’s student (http://csc165ftw.blogspot.ca), I sometimes look at his SLOG because he will include diagrams like this:

Problem solving episode:
Step 1: In the above question, let’s assume f(n) = 2^n and g(n) = n^2. The graph shows that f(n) grows more rapid than g(n). Therefore 2^n/n^2 approaches infinity as n approaches infinity. Also, we two other functions f(n)/g(n) are to approach 0 as n approaches infinity, we know that f(n) grows slower than g(n).
Step 2: To prove that, for example, f(n)/g(n) approaches infinity, we can use L’Hopital’s Rule, where we can derive f(n) and g(n) up until it’s obvious that their ratio approaches infinity. Once this is shown, we can assume the following statement to help us with our general proof:

This is the definition of limit in “statement” form, applicable only if f(n)/g(n) approaches infinity (if it approaches 0, then the last part of the statement should be f(n)/g(n) < c, since we can find any number c beyond a breakpoint n’ where the ratio is going to be smaller than that number c).
Step 3:

Step 4: Looking back at the proof, we know that since we are trying to disprove the statement 2^n ∉O(n^2), we only get to choose n, therefore we can introduce c and B at the beginning. Comparing to proving the statement, we need to introduce B after proving the limit and then making B depend on n’ so to make the statement easier to prove.

csc165 – week 8

This week, we learnt about  Big O. Big O is the symbol that computer scientists use to show the upper bound of function’s step. In other words, it is the maximum steps that a function can reach(over-estimation). In symbolic form, it looks like this.

To understand this complicated statement, we should separate it into small parts. The first part is saying that it takes natural number as input and returns positive real number. There is constant c which is positive real number and B a natural number that for all n if n is greater than B f(n) is equal or smaller than c * n^2 . B is the natural number that is n’s minimum in this statement, and c is the multiplier that makes f(n) always smaller  c *(n^2).

Problem solving episode:
Step 1: Write a detailed structured proof that 
Step 2: What is the proof structure of Big-O?

We have to first work from LHS to get the value c.

Step 3: Now plug in the ^ above argument and make it into a complete proof:
Step 4: Looking back, what is the most difficult part of the proof? The working forward and backward to get that c value really, in step 3 we are just merging what we have done (and reasoning i know…). For the scratch work, be careful the power and always keep in mind that Big O is the Upper limit that a function could reach.

So in proofing Big O, just be careful the inequality sign, whether the question is asking for a greater than (Big Omega) or smaller than. After all, Big O is less complicated than previous proofs if you are not scared by the complicated symbols. Keep in mind the definition of Big O and it shouldnt be great deal.

csc165 – week 7

This week, we start reading legit python code for the first time. Python is the first and only programming language I know and so I am quite excited to see it appear on our lecture notes. We had a little activity called the “penny piles” on Friday and it is about sorting. In csc108, we learnt about 3 different kinds of sort. We learnt the algorithms and how to write their codes. However in csc165, we focus on the METHOD of sorting (we will talk about the activity later). In the lecture though, Prof Heap did introduce the algorithms of insertion sort and selection sort AND ALSO walked us step by step through the python code so we understand how python runs it and *HOW LONG does each take. Here’s the conclusion: in worse case scenario, code has to run almost every line -> the “IF” condition suits most of the criteria in early lines.

Problem solving episode:
Step 1: Left drawer contains 64 pennies, right drawer contains 0 pennies. how to arrange them in a way that one of the drawer has 48 pennies under the condition that: if a drawer has even number of pennies, transfer half of them to the other drawer; if a drawer has odd number of pennies, you can do nothing.
Step 2: Under the condition, I should try making the pennies to be even in that way I could further divide the pennies.
Step 3: Draw a circles and start dividing…
A: 64 B: 0
64/2 = 32
A: 32 B: 32
32/2 = 16
A: 16 B = 32+16 = 48! <DONE>
Step 4: Did I violate the conditions? No. Did I get what I want? Yes.

csc165 – week 6

This week is thanksgiving week. We did more proofs and proofs by parts is introduced where you have to split the proofs into many parts then use conjunction to summarize different parts. In previous weeks, the idea of conjunction is introduced and this week we get into details of how to manipulate it.

Problem solving episode:
Step1: Proof ∀n ∈ N n is odd => n^2 is odd
Step2: know the definition of n: n must be odd natural numbers, n also will be odd even when adding 1 to
Step3:
Assume n ∈ N #n is generic natural number
Assume n is odd # assume antecedant
Then ∃k ∈ N n = 2k + 1 # Definition of n; n must be odd natural number
# n will be odd since you are adding 1 to even’s multiples.
Then n^2 = (2k +1)^2 # substitution; n as def of odd
= 4k^2 + 4k + 1 # Expansion
= 2k(2k + 2) + 1 # Simplification.
Then n^2 is odd # Up to this part was hard but rest of proof are just structure.
Then n is odd => n^2 is odd # By assuming antecedant, derived consequent.
Then ∀n ∈ N n odd => n^2 is odd # Introduce ∀
Step4: notice that 2k(2k+2) + 1 looks very similar as definition of odd that we defined above. (def of odd: n = 2k + 1). Also, if we think (2k + 2) as k in def. of odd, we’re not vaiolating any mathematical rule since k is still a generic natural number. PROOF DONE! 😀

csc165 – week 5

This week, we are doing more proofs but focusing more on the floor function. Recall last week’s slog, I mentioned that every symbol comes with a very significant definition and that’s what week 5 keeps reminding me. When I am stuck on finding a relation between two steps, I will just look back to the definition and all of a sudden, it is solved.

Problem solving episode:

Step 1: 

Step 2: Proof the equality by showing: 

Step 3: use the definition of floor (given in the question) THEN think how to make LHS to look like RHS? We should start from x, using the floor definition to work out the relation:

Step 4: We successfully transform LHS to RHS using the definition of floor. One challenging thing about this question is to always remember these steps: 

These are the steps which majorly explain the relation between LHS and RHS.

csc165 – week 4

This week, we learnt about proving a claim about a sequence. A sequence means there is a comparison between two terms in an equation, for instance |P| > n. Also, the floor and ceiling concepts are introduced. The tutorial of this week is mostly about proofs using more of the definition, and every time when i am stuck on proofing a part, I will keep reminding myself what is the definition of a term and what is the relationship between the two terms.

Problem solving episode:
Step1: problem: write proof structure of
Step2: plan: what should a proof structure look like? If it is for all: assume something, then conclude something; if it is for some: let something to be something then conclude something
Step3: carrying out the plan:

Step 4: examine the solution: the proof structure includes both LHS and RHS parts and we also introduce the ‘imply’ relationship to link the two equations, finally introducing for all make our proof a complete solution

I was somehow ‘afraid’ to see such complicated slab of equations. But knowing how the structure works, it is easy and clear for me to follow the steps and I am impressed by the logical way (separating a long line into pieces and proof it bit by bit from left to right, THEN find relationship between two equations -> summarize) in proofing equations.

csc165 – week 3

This week, we went into details of the meanings and how to use the symbols. For instance, what does “imply” mean (both in english and in computer science) and what should be its negation. One thing that frustrated me a little is: some concepts seem really easy for us to understand in english, the meaning is obvious and so you thought its negation is just the opposite; however having learnt this lecture, it might be a total different story.

Problem solving episode: bi-implication

Step1: problem: (P->Q) & (Q->P)
Step2: plan: first we have to translate bi-implication into the conjunction of two disjunctions; then change the expression into disjunction of two conjunctions
Step3: carrying out the plan:
Step4: examine the solution:

After this week, I have a better understanding of the symbols and in the first assignment, the biggest challenge is to type the answers in! I will work hard on that.